Practical Techniques for Searches on Encrypted Data

论文信息

• 发表: IEEE Symposium on Security and Privacy (CCF A, 2000)
• 阅读目的: 了解它是怎么在密文中搜索的, 找网络数据包传输过程中如何检测被修改的idea.
• 作者使用的思想为A XOR B XOR B = A, 但本文是第一篇提出在在密文中搜索. 略过所有数学证明和背景介绍.

应用场景

Alice 要存储文档到Bob的服务器中, 此时只能存储密文, 因为Alice 并不放心Bob. 但这时, Alice 想要返回所有包含词’W’的文档, 这时就需要Bob在加密的文档中搜索.

方案1: 基础方案

假设想要加密的文档有\(W_1, W_2, …, W_l\)个单词.

加密: Alice 要想加密, 就先使用伪随机数生成器G生成一个随机数序列\(S_1, …, S_l\). 每个\(S_i\) 有 n-m bit 的长度. 要对每i个位置的单词\(W_i\) 加密, Alice首先生成一个\(T_i = <S_i, F_{k_i}(S_i)>\)(\(<\cdot, \cdot>\)表示比特连接), 并获得该单词的加密结果: \(C_i := W_i \oplus T_i\). 因为只有Alice 能生成 \(T_1, …, T_l\), 所以这个方法是相对安全的.

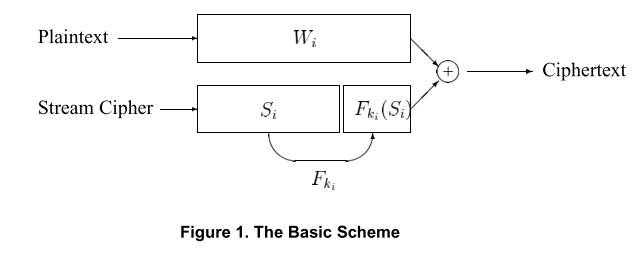
查找: 想要搜索单词W, Alice需要将W, 以个W可能出现位置对应的\(k_i\)发送给Bob. Bob通过检查\(C_i \oplus W_i\) 是否等于一些\(<s, F_{k_i}(s)>\)来进行对加密文档的搜索.

缺点: Alice会向Bob暴露单词W,以及所有的\(k_i\). Alice需要事先知道W可能出现的位置.

方案2: 控制搜索

加密: 这里的控制主要是在密钥生成上面, 将原来每个位置i对应一个\(k_i\)密钥改成\(k_i := f_{k’}(W_i)\), 这里它把这个单词的密钥与这个单词是啥给结合了起来, 而\(k’\)只有Alice自己知道. 其他方面与方案1是相同的.

搜索: Alice将W和\(f_{k’}(W)\)发给Bob, Bob在每个位置都搜索一次即可. 当\(W_i=W\)时, Bob可以搜索到, 当不相等时,则搜索不到信息, 因此这个方法可以避免位置信息泄露. (这里我觉得对所有的S, 都要计算出\(T_i\), 再将\(C_i \oplus W_i\)的结果与每一个\(T_i\)作对比才行, 如果有相等的, 就说明这个位置的单词是W).

问题: 暴露了W给Bob.

方案3: 隐藏搜索

加密:要隐藏信息, Alice在存储前对明文作一次加密即可. 即对单词\(W_i\), 计算: \(X_i := E_{k’’}(W_i)\), 然后再生成密文: \(C_i := X_i \oplus T_i\). 这时搜索时, 只要将\(X_i\)给Bob, 所以不会泄露W的任何信息.

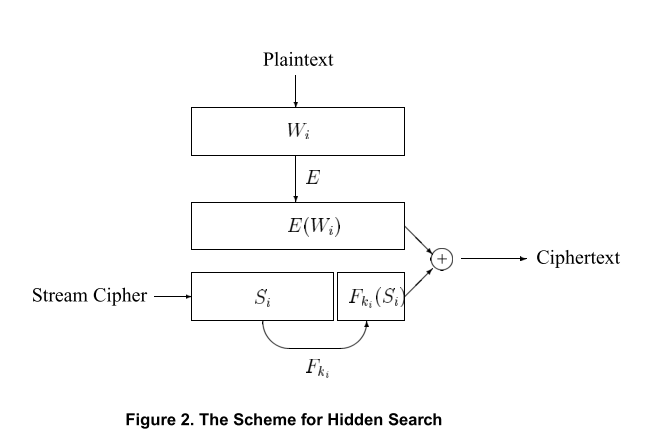
搜索: 与方案2相同.

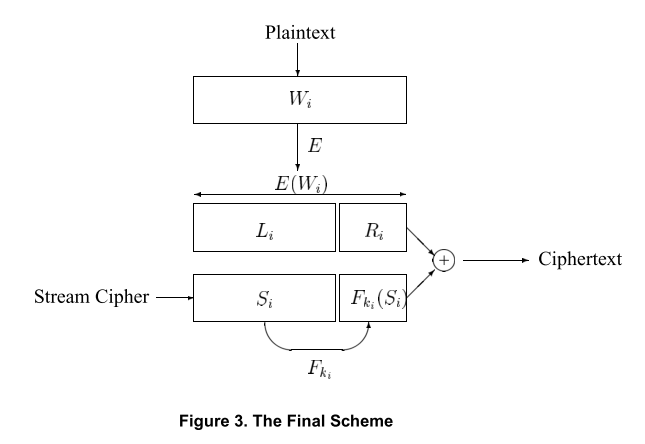
最终方案

前面方案的不足: Alice无法从Bob那里的加密文本获得原始文本, 因为还需要\(E_{k’’}(W_i)\)才能计算出\(k_i\).

加密: 将预加密单词分成两个部分: \(X_i = <L_i, R_i>\). \(L_i\)为前n-m个比特位. Alice生成密钥: \(k_i := f_k’ (L_i)\). 解密时, Alice利用\(S_i\)与\(C_i\)的n-m位异或来恢复\(L_i\), 从而让Alice计算\(k_i\)并完成解密.

解释: 因为\(T_i := <S_i, F_{k_i}(S_i)>\), 而\(C_i := T_i \oplus X_i\), 这里的\(X_i = <L_i, R_i>\). 这时将\(S_i\)与\(X_i\) 的前(n-m)位异或,即可获得\(L_i\), 又能根据\(L_i\)计算得到\(k_i\), 从而完成解密.