马尔可夫决策过程 (Markov decision processes,MDP)

马尔可夫过程

参考自这里

性质(Markov Property)

马尔可夫性质指的是: 未来只与当前状态有关，与过去无关。可以使用以下定义:

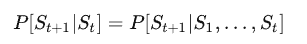
可以从这个式子里面看到, 下一个状态为\(S_{t+1}\)的概率只于当前状态\(S_t\)有关, 而与更前的状态\(S_1, S_2, …, S_{t-1}\)都无关.

我们对当前状态和后续状态分别记为\(s, s’\), 从当前状态转移到后续状态的转移概率定义为:

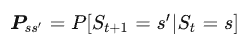
对于一个马尔可夫过程如果有n个状态, 那这些状态互相转换则共有\(n^2\)种转移, 将这些转移过程记为一个转q称矩阵:

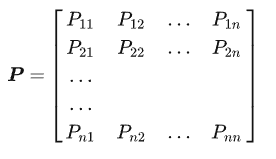
马尔可夫过程 (Markov Process)

记一个随机过程中:

• S是有限数量的状态集

• P是状态转移概率矩阵

• 它具有马尔可夫性质

• 转移概率不会随时间变化

则它是一个马尔可夫过程, 表示为\(<S,P>\).

以下例子: 一个学生所处状态的随机过程

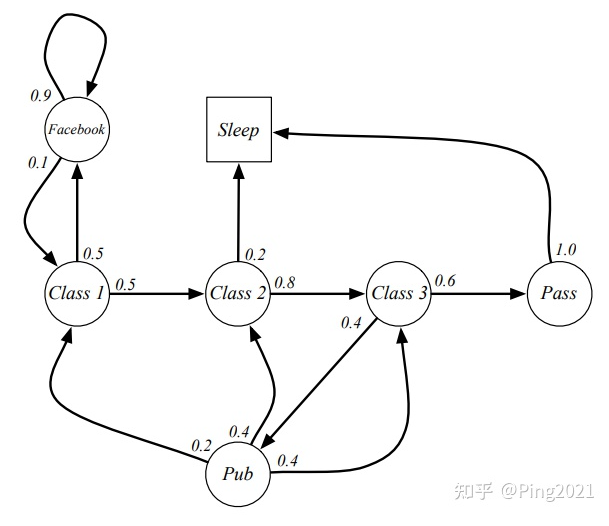
这里每一个球就是随机过程中的一个状态, 箭头表示状态转移, 箭头上的数字表示转移概率. 比如学生在Facebook这个状态, 那他有10%的概率会去Class 1 学习, 90%的概率会继续玩Facebook.

以下是可能的状态转移过程:

C1 - C2 - C3 - Pass - Sleep

C1 - FB - FB - C1 - C2 - Sleep

C1 - C2 - C3 - Pub - C2 - C3 - Pass - Sleep

C1 - FB - FB - C1 - C2 - C3 - Pub - C1 - FB - FB - FB - C1 - C2 - C3 - Pub - C2 - Sleep

这个随机过程的转移概率矩阵为:

马尔可夫奖励过程(Markov reward process)

这部分的题目比上部分多了一个奖励, 因此内容上也一下, 和马尔可夫随机过程相比,我们在每一个状态上添加一个奖励.

先摆上给每个状态添加奖励后的随机过程的一个图示:

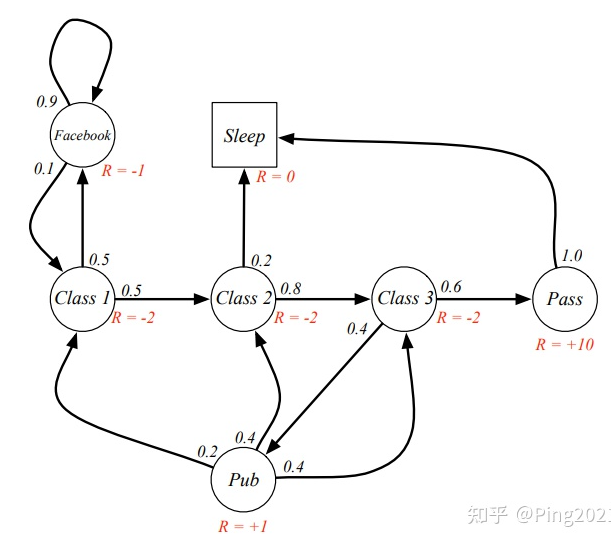
马尔可夫奖励过程表示为: \(<S,P,R,\gamma>\)

• S是有限数量的状态集
• P是状态转移概率矩阵
• R是一个奖励函数，\( R_{s} = E[R_{t+1} | S_{t} = s] \)
• \(\gamma\)是一个折扣因子， 其取值范围为: [0, 1]

奖励函数

离开当前状态所获得的奖励,记为\(R\).

用上面的图举个例子, 假如学生当前在状态Class 1, 此时他即可能进入Class 2, 也可能进入facebook, 不管他下一个状态进入的是哪个, 他离开Class 1状态都会获得 -2 的奖励, 也就是进入下一个状态时, 会获得本状态的奖励.

折扣因子

折扣因子记为 \(\gamma \in [0,1]\), 当我们用它来计算未来收益时会乘以折扣因子, 比如在Class 1 进入facebook和进入 Class 2后虽然当前的收益是相同的, 但未来收益是不同的. 引入折扣因子的原因:

• 首先，数学上的方便表示，在带环的马尔可夫过程中，可以避免陷入无限循环，达到收敛。
• 其次，随着时间的推移，远期利益的不确定性越来越大，符合人类对于眼前利益的追求。
• 再次，在金融上，近期的奖励可能比远期的奖励获得更多的利息，越早获得奖励，收益越高.

收益 (Return)

定义为: 从当前时刻起经达 k+1 时间步骤后获得的带折扣奖励总和, 即:

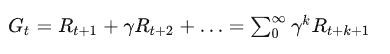
例个例子:

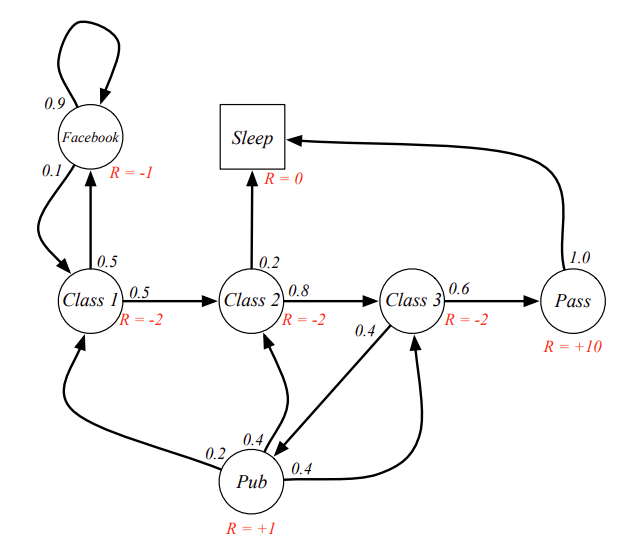
在这个马尔可夫过程中, 各状态奖励为:

因此对于采样获得的马尔可夫链能获得的收益为:

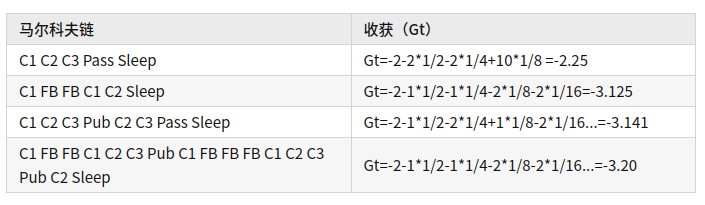
价值函数(state-value function)

从该状态s开始的回报的期望, 它表达的是某一状态的长期价值, 记为\(V(s)\), 表达式为:

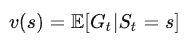
比如对于如下马尔可夫过程:

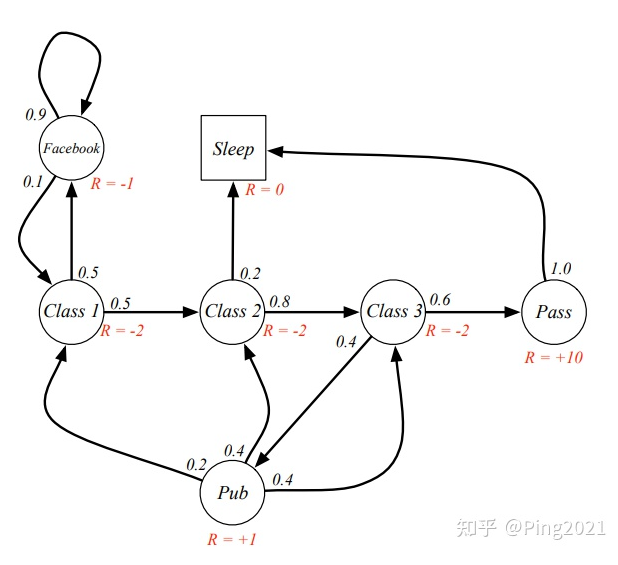
我们将每个状态价值函数的初始值设为0

FB状态时，有0.9的概率进入FB,0.1的概率进入到C1，因此

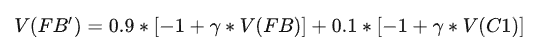
Pub状态时，有0.2的概率进入C1,0.4的概率进入到C2，0.4概率进入C3，因此

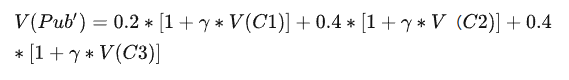
同理,其他状态价值函数:

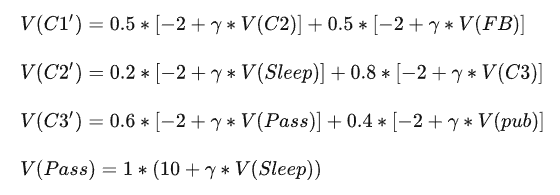
根据上面公式，进行迭代计算V值。各状态的初始V值都设0，算出各状态的后续状态的V(S’)值, 再将算得的V(S’) 作为下一个状态的初始值V(S).

因此可得:

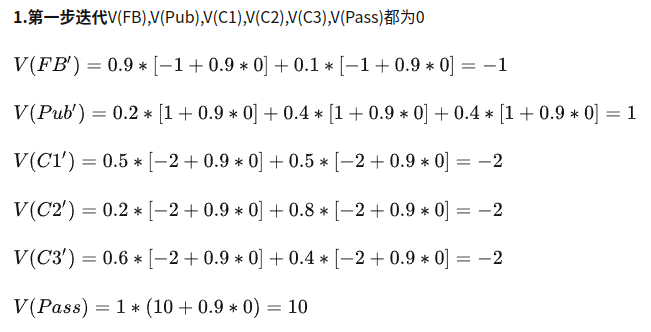
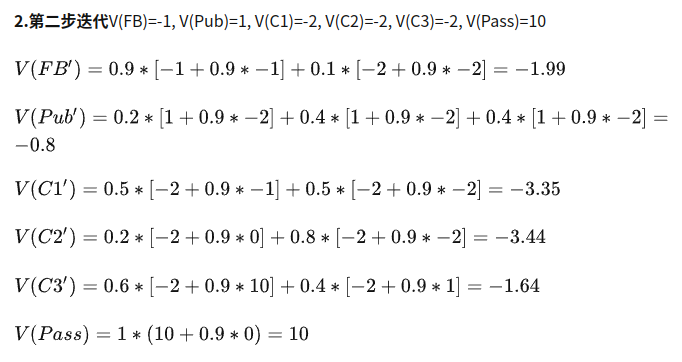
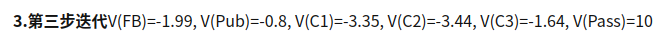
如此下去,直到稳定.

MRP的贝尔曼方程（Bellman Equation for MRPs）

推导过程就不列了, 涉及到了不大懂的知识, 将最终的方程列一下:

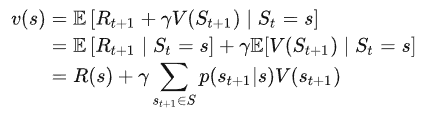
这个式子还是很好理解的,结合前面的例子,当前状态的收益为当前状态的价值+\(\sum\)下一个状态的转移概率X下一个状态的价值 X \(\gamma\). 可以用下面这个图形来解释:

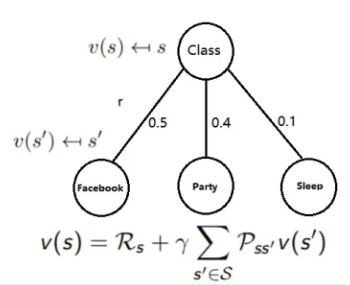
它还有矩阵形式, 就不列了, 这里的用处不大, 原博客上都有

马尔可夫决策过程（Markov decision process）

马尔可夫决策过程是在马尔可夫奖励过程的基础上加入了动作, 定义为: \(<S,A,P,R,\gamma>\)

马尔可夫决策过程的状态转移概率和奖励函数不仅取决于智能体当前状体，还取决于智能体选取的动作, 而马尔可夫奖励过程仅取决于当前状态。

策略 (Policy)

它是一个对于给定状态s时, 其动作a的分布, 记为:

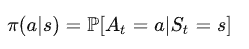
它定义了智能体的行为方式, 即各种状态下采取各种动作的概率(采取不同的动作即会转移到不同的状态)

MDP的策略仅与当前的状态有关，与历史信息无关；同时某一确定的策略是静态的，与时间无关；但是个体可以随着时间更新策略。

由于状态转移会与不同的策略有关, 因此某个状态的收益也与策略有关.

价值函数 (Value Function）

贝尔曼期望方程（Bellman Expectation Equation）

备份图（backup diagram）

最优价值函数（Optimal Value Function）

贝尔曼最优方程（Bellman Optimality Equation）

马尔可夫决策过程的扩展

其他类别的MDP有：无限状态和连续MDP；部分可观测MDP；不带折扣的、平均奖励MDP等