Hoeffding's inequality (霍夫丁不等式讲解)

霍夫丁不等式表达

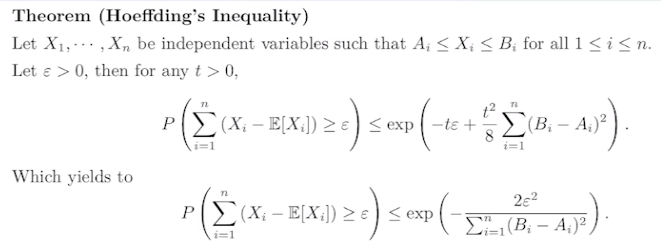
下面的这个式子是我们常用的

Markov inequality

一个取值非负的随机变量\(X \ge 0\), 有不等式 \(P(X \ge \epsilon) \le \frac{1}{\epsilon} \mathbb{E}X\).

这个不等式的证明:

过程中使用了微积分和一些不等式的基础, 不了解了.

Jesen inequality

对于突函数而言的一个不等式

均值不等式

这里使用的其实是对\((a - b)^2 \ge 0\)的变换, 最终得到\((a+b)^2 \ge 2 \sqrt{ab}\).

霍夫丁不等式的证明

首先使用\(Y_i = X_i - \mathbb{E}_i\) 来替换原不等式, 得到新的需要证明的式子: 这里变换后\(Y_i\)的聚会范围变了, 我们设它的聚会范围为: \(a_i \le Y_i \le b_i\)

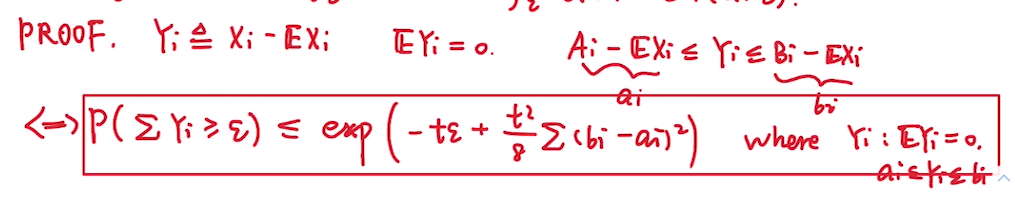
这里要对上面方框中的式子使用马尔可夫不等式来放缩,但由于我们并不能保证 \(\sum Y_i \ge 0\), 因此使用e的指数对原式进行变换, 结果如下:

这里由于\(Y_i\) 是独立同分布的, 因此可以做变换 \(e^{-t\epsilon} \cdot \mathbb{E}[e^{t \sum Y_i}] = e^{-t \epsilon} \cdot \prod \mathbb{E}[e^{t Y_i}]\)

根据\(Y_i\)的取值范围, 我们利用\(\alpha\)来修改\(Y_i\)的表达:

再将修改后的表达带入\(e^{tY_i}\) 得:

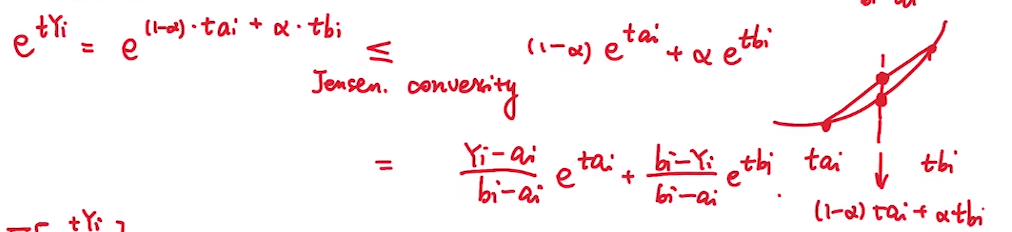
这里使用了杰森不等式进行了缩放

所以利用杰森不等式和\(\alpha\)的缩放, 我们可以对\(\mathbb{E}[e^{tY_i}]\)进行缩放得下式(记为*):

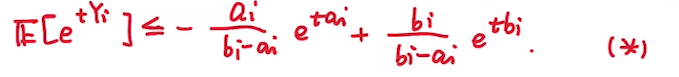
这里引入两个变量\(\mu, \gamma\)

再将这两个变量带t主(*)式得:

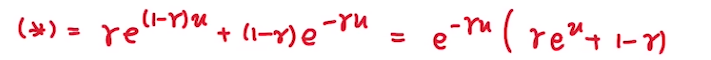
此时再将变换后的(*)式取对数,并记为\(g(u)\)得如下式:

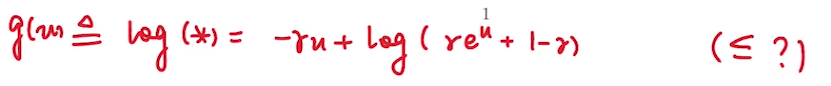
此时我们想对\(g(u)\)在0处进行泰勒展开, 所以我们对它进行求导再计算其自变量为0时的值, 在其二次导入使用均值不等式进行缩放,计算如下:

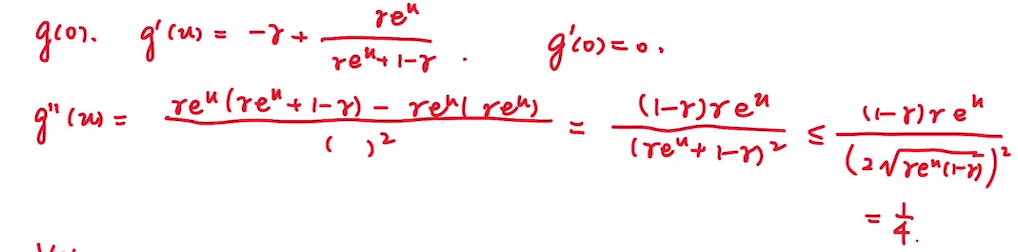
此时对\(g(u)\)进行泰勒展开,借助拉格朗日余项得:

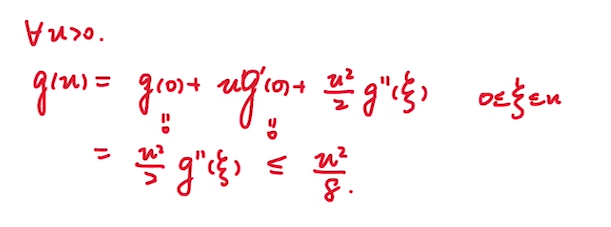
这里的缩放利用了上面二次导的缩放.

我们获得了\(g(u)\)的界, 根据\(g(u)\)的定义以及(*)式, 我们可以得到:

此时再带入最被的式子可以得到\(P(\sum Y_i \ge \epsilon)\)的一个不等式:

上式的右侧是一个关于t的二次函数, 因此对右侧取\(t > 0\)时的最小值可得:

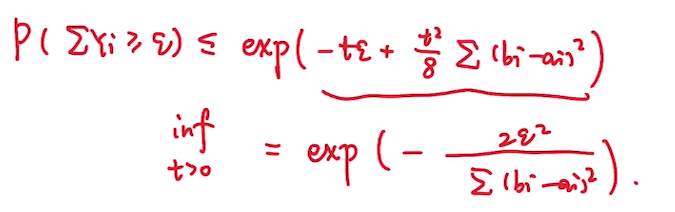
得证.

将上式还原成\(X_i\)的形式即可得到最原始的霍夫丁不等式.

以上参考自: 参考链接

将霍夫丁不等式应用在伯努利两点分布的特例

有独立随机变量服从伯努利分布, 即某个变量取1时概率为p, 取0时概率为(1-p), 则它满足的霍夫丁不等式如下:

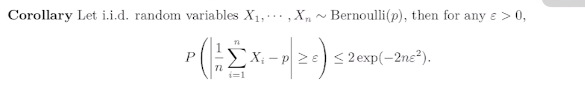
上式其实表达的是均值依概率收敛于p

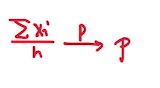
对于不等式中的绝对值展开成两部分

先看正的部分, 原式展开并带入霍夫丁不等式即得:

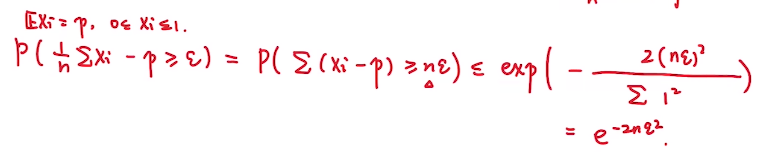
再看负的部分:

令\(Y_i = - X_i\) 并替换原式可得:

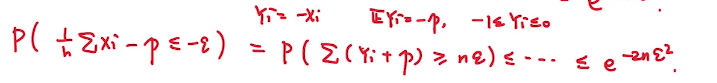
所以将两个式子合在一起就得到了

原来的不等式证明.

论文中涉及到的

ShortMAC: Efficient Data-Plane Fault Localization, NDSS

论文中的引理一: 恶意交换机注入一个数据包会被检测到的概率为q, 设一个阈值\(T_{in}\). 若要保证被检测到的包数少于域值\(T_{in}\)的概率不多于\(\delta\), 那么恶意交换机注入的包数不多于:

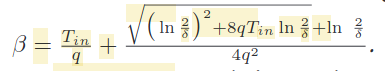
完整描述如下:

给定的证明如下:

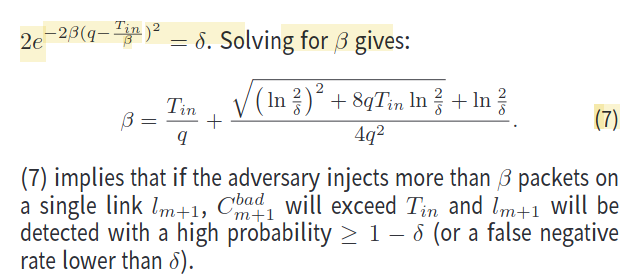
照原文的说法, FN的概率 \(\mathbb{P}_{fn} = \mathbb{P}(C_{m+1}^{bad} < T_{in})\), 即被检测到的数量未到达阈值.

这里我按照我的理解推导了一下式(6), 首先建模为伯努利, 记注入的数据包为随机变量\(X_1, X_2, …, X_y\), 被检测到的概率为q, 所以这里记随机变量\(X_i\)为1的概率为q. y个这样的随机变量出现1的次数小于阈值的概率即为式(6)中的FN概率, 表达如下:

\[P(C_{m+1} ^{bad} < T_{in}) = P(\sum X_i < T_{in})\]

文中提取了利用霍夫丁不等式, 因此我们把上式右侧做些变换:

\(P(\sum X_i < T_{in}) \)

\(= P(\sum X_i - qy< T_{in} - qy )\)

\(= P(\sum (X_i - q) < T_{in} - qy )\)

\(= P(\sum (X_i - q) < -(-T_{in} + qy ))\)

在上面这个式子中, 由于这是一个伯努利分布, 因此\(q=\mathbb{E}X_i\), 所以它已经符合霍夫丁不等式的形式, 其中\(-T_{in} + qy\)即为\(\epsilon\), 因此利用这个不等式算这个概率的上界:

\( P(\sum (X_i - q) < -(-T_{in} + qy ))\)

\(= exp(- \frac{2(qy - T_{in})^2}{\sum 1^2})\)

\(=exp(-\frac{2}{y} (qy - T_{in})^2)\)

\(=exp(-2y (q - \frac{T_{in}}{y})^2)\)

可以看到这里的结果比式(6)少了一个2倍, 不知道是谁的公式出了问题 .