Dynamic Packet Forwarding Verification in SDN
affliation and publication
-
author: Qi Li, XiaoyueZou, Qun Huang, Jing Zheng, Patrick P.C.Lee
-
publication: IEEE Transactions on Dependable and secure computing, 2019
-
abs
传统方法无法应用到SDN中的原因: SDN 中的交换机功能太少. 作者提出: 使用控制器收集包和流的统计来判定包是否被修改, 交付路径是否正常; 并对该方法加以改进
- 与我的不同点:
- N-pfv中每一个包都要利用packetIn送到控制器进行完整性检测, 应该不可取
- 每个rule 都有一个timer, 如何在数据平面利用过期的包触发控制平面对path的完整性检测呢?
- 每个rule结束时都会有一个统计请求.
- 对每个流都要有一个hash表(\(P_i\)表).
- 抽样检测中如何使egress对ingress相同的抽样出来的包进行packetIn?
- 若使用流表的过期时间控制, 那就得不停地下发流表.
- (是我当时没看懂, 使用流表控制packetIn, 用概率参数\(\lambda\)确定当前是否下发流表, 不下发就会有packetIn, 下发就没有)
- 使用的工具,或许有用:
- CAIDA数据集
- 拓扑
- 用于模仿dropping攻击的ovs-ofctl tool
- 用于模仿injection攻击的TCPreply
Introduction
- p1: 指出交付异常检测的重要性
- p2: IP网的解决办法,不足及为何不可用于SDN
- p3: 提出一个方法, 并用其有可行性引出challenge
- p4: 本文的方法及贡献
Problem Statement
Basic of SDN
Threat Model
- packet hijacking attacks. 对包改路
- packet delaying attacks. 延迟
- packet injection attacks. 攻击者向流中加入包
- packet dropping attacks. 丢流流的包
- packet tempering attacks. 修改包
- hybrid attacks. 丢一些包再复制或注入同等数量的包
表1 是对当前研究方法对这些问题的解决情况:

本段剩余内容: 分析已存在方法且无法用于SDN; 本文要解决的问题及假设.
Packet Forwarding verification
Design goals
Novel Packet Forwarding Verification (\(\mathcal{N}\)-PFV)
当包在进和出交换机时都生成 packetIn 包以确定交有没有修改;控制器定时检查包的统计信息以确定包是否交付异常. 因此产生了2个问题:
- 如何交付包到控制器
- 中间节点何时报告统计信息
文中使用的标记见表2
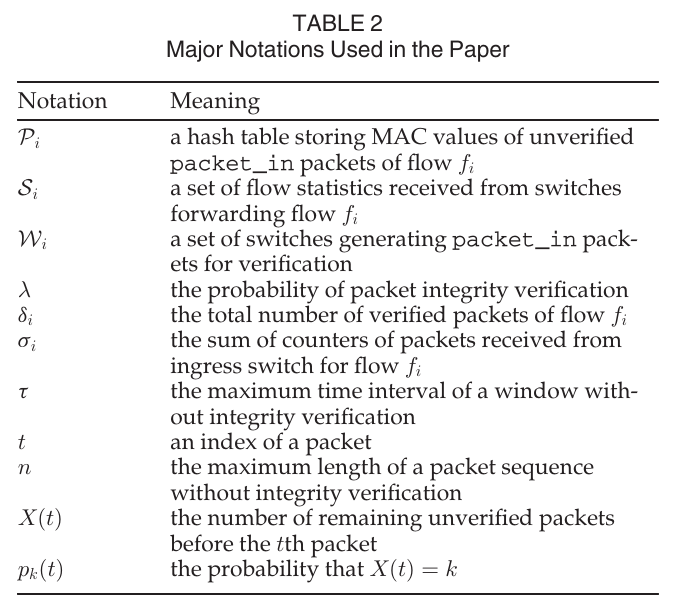
PFV的整体overview见图2:
PFV 算法见算法1

\(N\)-PFV作为NOS的一个模块运行在控制器中, 算法 1 中1-12行为NFV验证包的完整性.
- 对每个从ingress来的包计算它的Message Authentication Code (MAC), 并将其存入一个hash表中(每个项都有超期时间)
- 对从egress来的包计算它的MAC, 并从hash表中将对应的删除并增加已验证包的计数\(\delta_i\)
- 如果从egress的MAC无法与hash表中的匹配,定位这个交换机 7-9
- 若被匹配的包与总的hash个数之比小于\(\theta\), 验证失败, 定位恶意交换机 10-19
- 当rule过期, 就检查数据平面这个rule对应所有流表的连续性, 以确定当前攻击. 不同: 每个rule都有一个timer; 每个rule最终都会触发一次流状态请求
图2中的例子中,从A中进入的包会触发packetIn, 从C中出去的包也会.若最后2个PacketIn包相等则通过验证,否则让B生成PacketIn, 若此时相等则证明链路B-C安全. 若控制器中有rule过期则收集ABC的流表并比较. 如图2中可见B有恶意行为因为他的统计信息比A少. 若此时控制器中没有MAC过期则 packet hyjacking, 否则 dropping. 可见PFV可以有效地定位恶意交换机.
Discussion
Enhanced PFV: DynaPFV
DynaPFV 通过随机抽取flow中的包并生成packetIn来降低检测代价。当收到packetIn包时以概率\(\lambda\)确定下一个包是继续检测完整性还是下发流表. DynaPFV过程见算法2, 若收到packetIn包或所保存的hash中有过期的,则以一定的概率进行包完整性检查。若检查,下发检查流表(会触发packetIn)否则下发随机过期时间的流表(流表过期会触发行为检查)。

Dynamic Packet Verific
ation 具体算法过程可见算法3.

当从ingress中收到某个流\(f_i\)的PacketIn包时, 就为它计算MAC并将其存入hash表\(\mathcal{P}_i\)中. 当从egress中收到时就计算MAC并从对应的hash表中移除并增加验证成功包的计数. 每次移除都降低抽样概率\(\lambda = \lambda * \alpha\), 若有MAC过期则增加抽样概率\(\lambda = \frac{\lambda + 1}{2}\). 若匹配包数与总包数之比小于\(\theta\)则认为异常从而定位异常交换机. 此外初始值设定\(\lambda = 1, \alpha = 0.99\). 最后用图3来说明对上述过程举例.
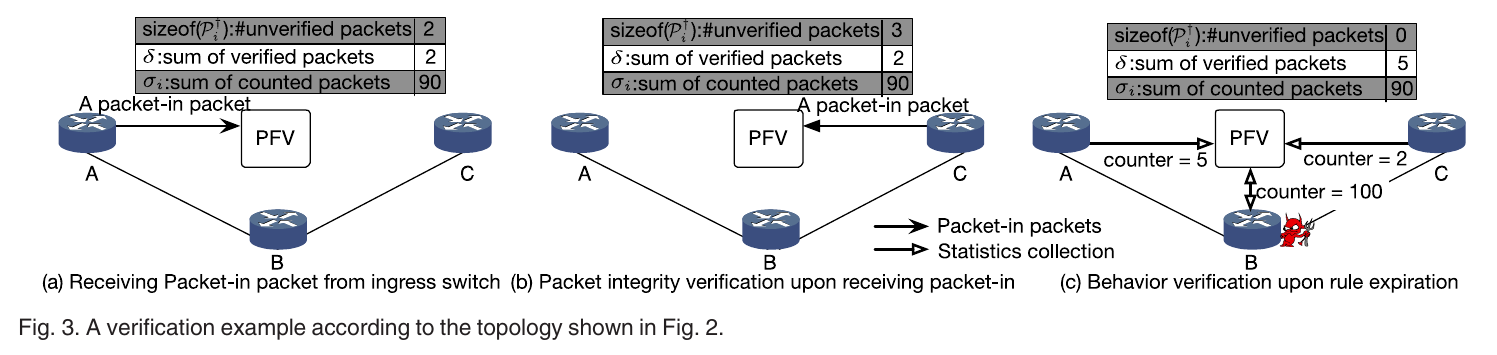
Dynamic Behavior Verification
下发流表的过期时间是随机的,流表过期会触发行为检查,因此检查的间隔也是随机的.检查过程如算法4所示:

对path上的交换机处理的包进行统计, 并都与ingress交换机的统计结果求比值, 中间交换机直接统计, egress交换机则为统计结果加检查的包数\(S_i[0] + sizeof(\mathcal{P}_i + \sigma _i)\). 比值大于\(\theta\)但小于1则提高抽样概率\(\lambda\), 否则减小\(\lambda\). 最后清空\(\delta_i\)和hash表, 并更新\(\sigma_i\)
Analysis
Detection Effectiveness Analysis
检测效果与\(\lambda\)有关, 未检测到的包序列取决与一个过期时间, 通过离散包序列, 未检测包序列的长度有限,可记为{1,2,…,n}, 因此我们可以将未检测的包序列建模为马尔可夫链, 未检测到的包序列升序服从于{1,2,…,n}中的一个正态分布. 本节将数据包与其剩余未检测序列的包数相对应, 当一个包被随机选中检测则认为剩余未检测序列的包数为0. 记\(X(t)\)为:当第t个包到达时该序列剩余的包数, 因此\(X(t)\)是一个随机变量. 我们可发现:
- \(X(t+1)\)只取决于\(X(t)\)
- 若\(X(t)\)非0, 则\(X(t+1)=X(t)-1\)
- \(X(t+1)\)以\(\lambda\)的概率为0, 或以\(1-\lambda\)的概率服从均匀分布:{1,2,…,n}
由一, \(\{X(t)\}\)形成一个有n+1个状态{0,1,…,n}的马尔可夫链.
记\(p_{k}(t)\)为\(X(t) = k\)的概率, 则\(X(t+1)=0\)的概率为\(X(t)\)为0且以\(\lambda\)触发或\(X(t)=1\), 因此可得:
\begin{equation} p_0(t+1) = \lambda p_0(t) + p_1(t) \tag{1} \end{equation}
同理,\(X(t+1)=k\)时(1). \(X(t)=0\), 下一个阶段不检测且新的不检测序列触发的是k个, 此时概率为\(\frac{1-\lambda}{n}p_{0}(t)\);(2). \(X(t)=k+1\), 此时概率为 \(p_{k+1}(t)\), 所以:
\begin{equation} p_k(t-1) = \frac{1-\lambda}{n}p_{0}(t) + p_{k+1}(t), 1 \le k < n. \tag{2} \end{equation}
再同理, 当\(X(t+1)=n\), 则\(X(t)\)一定等于0, 因此:
\begin{equation} p_n(t+1) = \frac{1-\lambda}{n}p_0(t). \tag{3} \end{equation}
此时, 第t个包被检测即\(X(t)\)为0, 概率为\(p_{0}(t)\). 因为\(p_{0}(t)\)无法被直接求得, 但它可被拓展:\( p_0(t+1) = \lambda p_0(t) + p_1(t) \tag{1}\), 再迭代替换\(p_{k} (t+1-k)\), \(1 \le k \le n\) , 就可以得到:
\begin{equation} p_0(t+1) =\lambda p_0(t) + \frac{1-\lambda}{n} \sum_{k=1}^np_0(t-k) \tag{4} \end{equation}
这个式子是不平凡的, 但仍可得到平稳概率:
\begin{equation} \lim_{t\rightarrow \infty} p_0(t) = \frac{2}{(1+n)(1-\lambda)+2} \end{equation}
图4展示了在不同的\(\lambda\)时每个包的检测概率
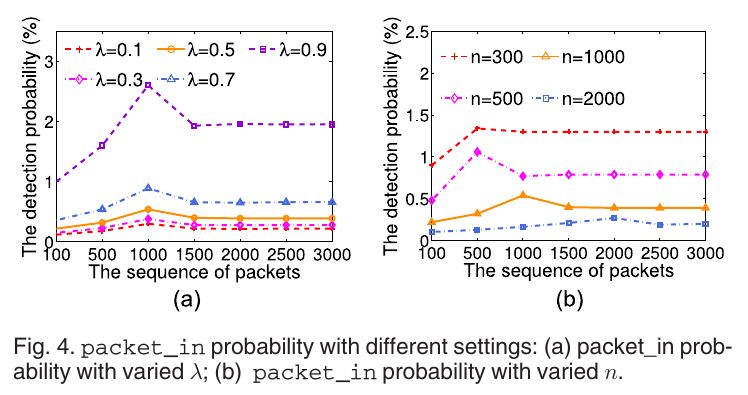
对\(\lambda\)的选择 不能太大,否则有太多的PacketIn包, 也不能太小,因为每个包的检测概率\(\frac{2}{(1+n)(1-\lambda)+2}\) 不能低于0.2. 因此在本文的算法中使用动态的\(\lambda\)选择法, 让其增长时不会超过1. 本文选择的初始值\(\lambda = 1, \alpha = 0.99\)
Security Analysis
主要讲了每种攻击是如何被检测到的, 可看原文
Performance Evaluation
在mininet和真实硬件上测试,所使用的trace从CAIDA\[2\]上获得
Implementation
- DynaPFV Mode 实现MAC及其定时功能
- Kernel Model 修改Floodlight, 使数据平面可以只接收packetOut而不接收修改流表操作
Experiment Setup
Mininet Experiment Results
每个主机生成250个流并每秒共生成1000个包 Experiment A1: Detection Accuracy 见图6a:不同的触发概率, 不同的攻击, 不同的篡改间隔, 不同的篡改持续时间
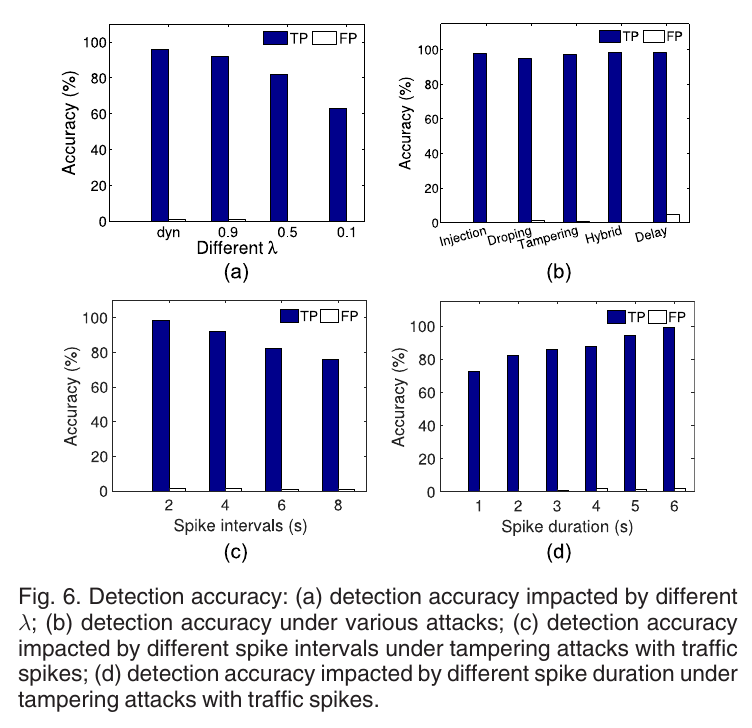
图6a是检测性能对不同\(\lambda\)的检测效果, 动态的效果更好.
Experiment A.2: Selection of \(\tau\): 实验结果如下:
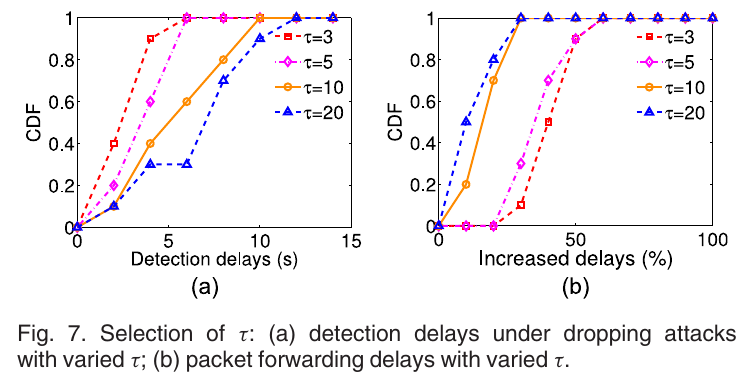
结果表明可以在6秒内检测出大多数攻击.
Experiment A.3: Detection Delay: 检测不同\(\lambda\)时的检测时延和流数与检测时延的关系, 结果见图8
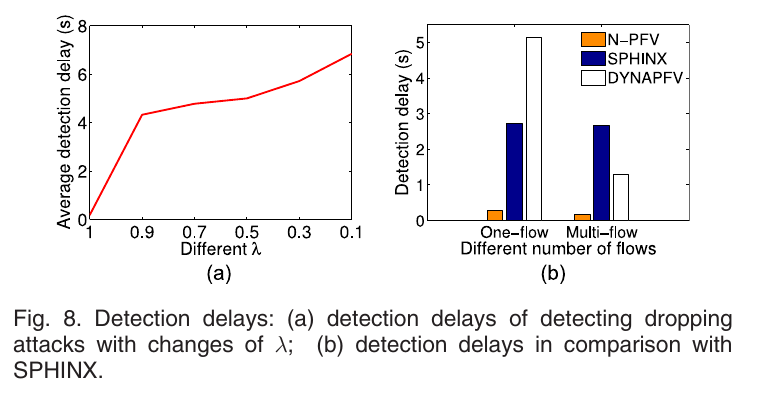
Experiment A.4: Overhead: 比较不同\(\lambda\)时packetIn的触发概率,导致的延迟和吞吐量的变化, 比较不同path长度时包的将会延迟, 检测结果如图9. 再没通信代价, 结果见图10
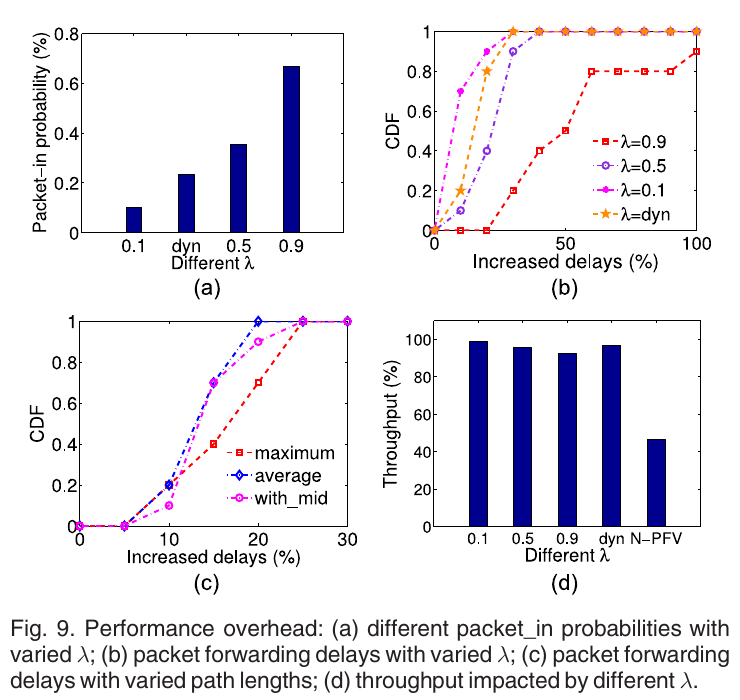
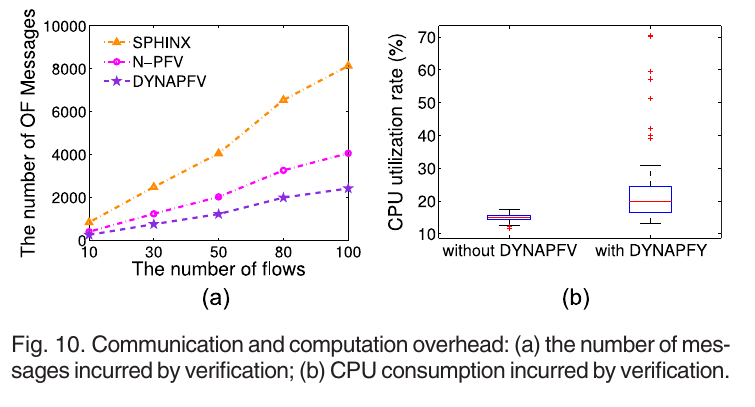
Hardware Testbed Experiment Results
使用4个EdgeCore AS4610-54T交换机, 使用 CAIDE数据集. Experiment B.1: Detection Delays: 不同的包率和不同攻击的检测延迟,CDF见图11:
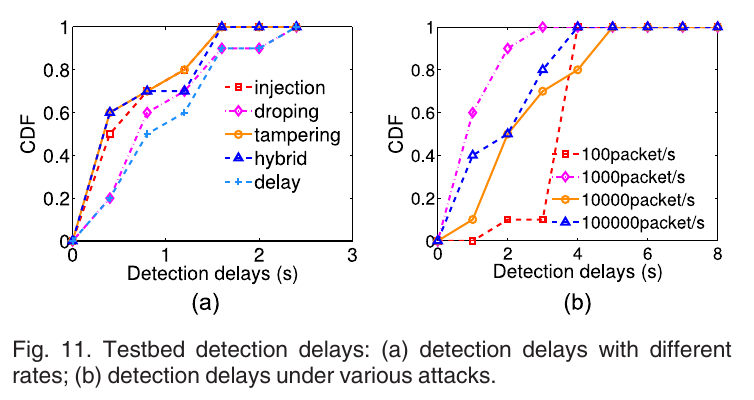
Experiment B.2: Overhead: 对包传输时迟的影响和吞吐量随\(\lambda\)的变化见图12:
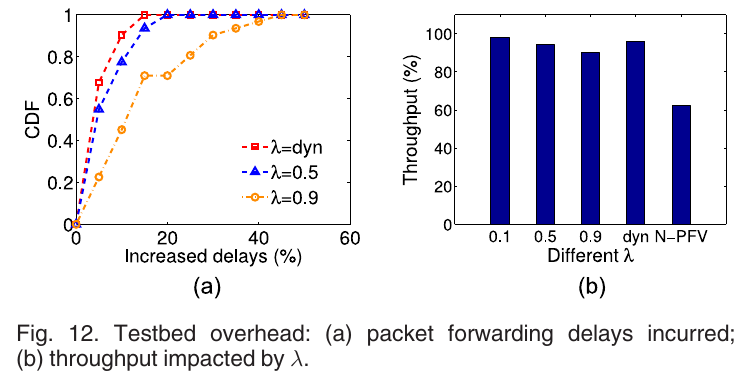
如果这篇文章帮到了你, 那就赞助我一瓶水吧, 这可以让我有动力去写更多的文章
Sponsor