Solving Minimum Path Cover on a DAG

文章目的

介绍一个用于在有向无环图（DAG）中进行最小路径覆盖（Minimum Path Cover, MPC）的算法。文中给定了一个场景（交通网络中的运输问题），并将这个场景建模成MPC问题，最后给出了求解方法。

情景样例

假设一个交通运输系统中有4个地铁站，站与站之间可达，交通时间表可确定。你需要做的是购买车票从而实现所有的运输。时间表如下：

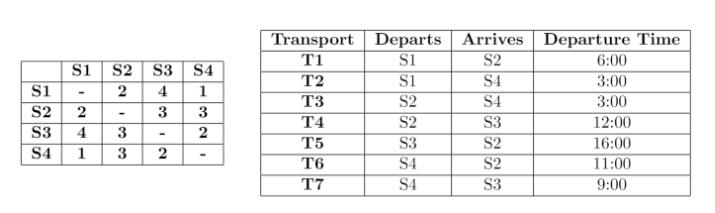
最坏的情况是每辆车都买一个票，需要7张。但其实有的运输任务可被同一个车完成，如T1和T2。我们需要做的是最大化运输效率，即最小化所构买的车票数，此时，找到了一个目标函数。

最优情况是一列车走过所有的站，这时只要买一张票即足够，这种情况不存在，因此我们把问题定义为：

最大化车所到达的站数的同时，保证所有的站点均到达。

首先根据传输时间表构造交通图，因为车辆到达时间是不同的且有先后的，所以车辆换乘是有时间依赖的，据此构造图如下:

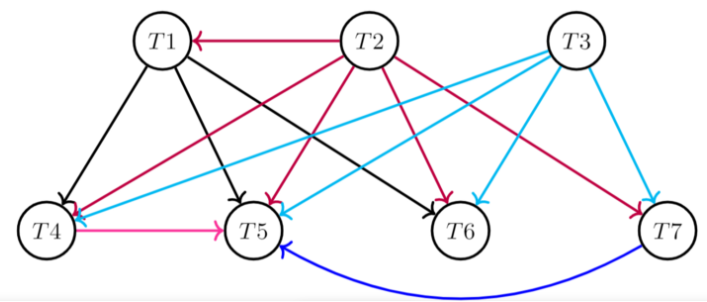
因此，现在问题转变为:

在以上构造的图上找到MPC。

解决办法

在通用的图上找MPC是一个NP-hard问题，但在DAG中找MPC可转换为找二部图的最大匹配问题，这可以在多项式时间内完成。

为解决以上问题，首先构造一个辅助图，在辅助图中，将原始图中的每个节点分为两个，一个节点保留原始节点的出度，另一个节点保留原始图的入度。举个例子，将节点$t$划分为\(t_1, t_2\). 对于t的邻居，从$t_1$画边连出去，对于将$t$作为邻居的其他节点，将该节点画边连到\(t_2\)。如此构造的图其实是一个二部图，结果如下:

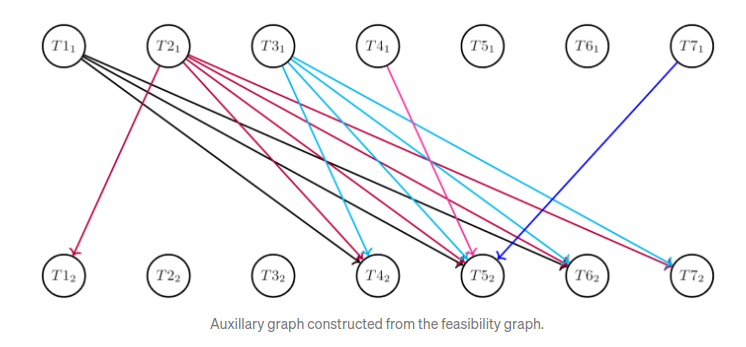
在以上二部图中查找匹配，假如找完最大匹配后某一个节点未到达，则需要单独为该节点购买一个车次的票以完成运输。因此最小化未到达节点的问题即是上图中的查找最大匹配的问题。而二部图的最大匹配问题是可以在多项式时间内完成的。

其中的一个匹配结果为：

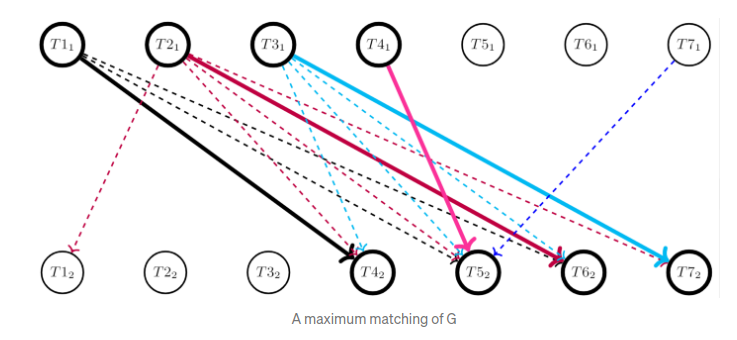
二部图最大匹配

对于二部图的匹配问题其是就是用匈牙利算法来解决的。这里简单介绍一下。参考自这里，这个作者还有其他算法的讲解以及代码实现。

对于现有的二部图

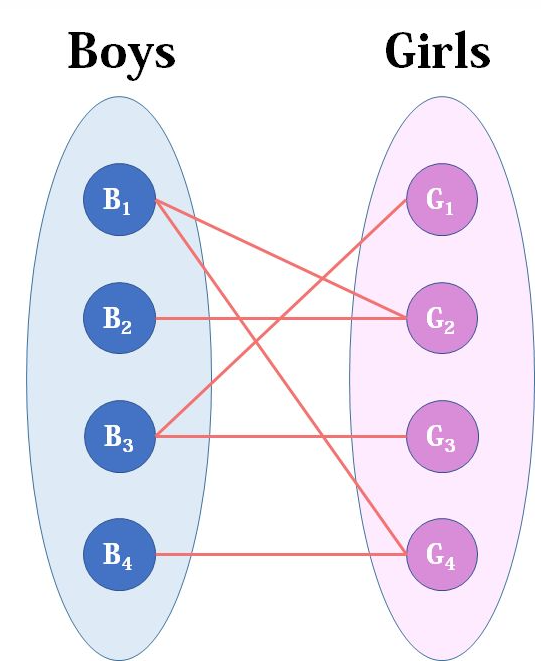
要找到它的最大匹配，是需要遍历它所有的节点的:

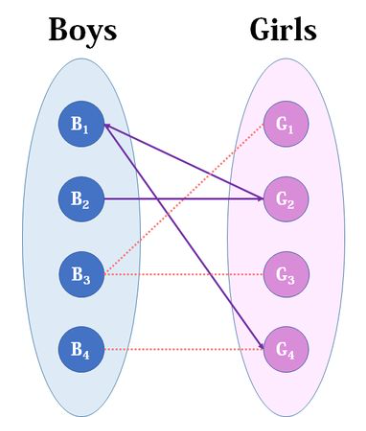
• 对于B1, 它与G2和G4都有连接，这里先将它与G2相连。

• 对于B2，它只与G2相连，这时再返回去看与G2相连的B1是否有别的相连的，可见G4可选，因此就将G2与B2相连，B1与G4相连；

  

• 对于B3，它与G1和G3相连，G1和G3都均未与其他节点相连，可将它连上G1

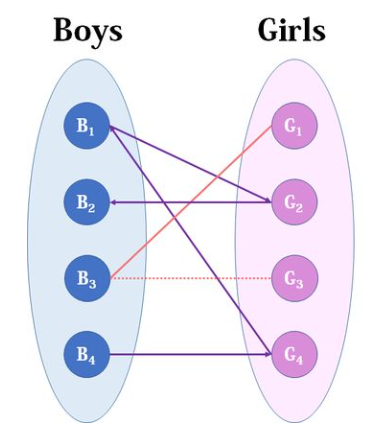
• 对于B4, 它只能与G4相连，但G4已与B1相连。B1除了G4，还可以与G2相连，但G2已与B2相连了，因此如果B4与G4相连了，B1就无法与别的节点相加，所以B4就无法匹配了。
• 至此，最大匹配结束。上述过程可见计算的复杂度是二部图两边节点之积。